GDAL Grid Tutorial
Introduction to Gridding
Gridding is a process of creating a regular grid (or call it a raster image) from the scattered data. Typically you have a set of arbitrary data scattered over the region of survey measurements and you would like to convert them into the regular grid for further processing and combining with other grids.
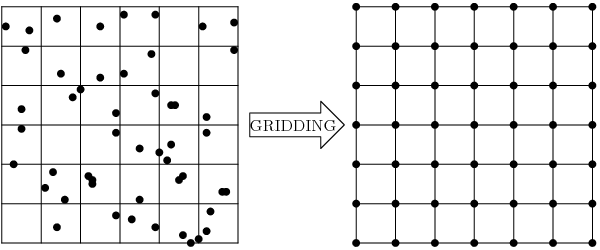
This problem can be solved using data interpolation or approximation algorithms. But you are not limited by interpolation here. Sometimes you don't need to interpolate your data but rather compute some statistics or data metrics over the region. Statistics are valuable themselves or could be used for better choosing the interpolation algorithm and parameters.
That is what GDAL Grid API is about. It helps you to interpolate your data (see Interpolation of the Scattered Data) or compute data metrics (see Data Metrics Computation).
There are two ways of using this interface. Programmatically it is available
through the GDALGridCreate() C function; for end users there is a
gdal_grid utility (which see for an up-to-date list of all current features).
The rest of this document discusses details on algorithms
and their parameters implemented in GDAL Grid API.
Interpolation of the Scattered Data
Inverse Distance to a Power
The Inverse Distance to a Power gridding method is a weighted average interpolator. You should supply the input arrays with the scattered data values including coordinates of every data point and output grid geometry. The function will compute an interpolated value for the given position in the output grid.
For every grid node the resulting value \(Z\) will be calculated using the formula:
where:
\(Z_i\) is a known value at point \(i\),
\(r_i\) is a distance from the grid node to point \(i\),
\(p\) is a weighting power,
\(n\) is a number of points in Search Ellipse.
The smoothing parameter \(s\) is used as an additive term in the Euclidean distance calculation:
where \(r_{ix}\) and \(r_{iy}\) are the horizontal and vertical distances between the grid node to point \(i\) respectively.
In this method the weighting factor \(w\) is
See GDALGridInverseDistanceToAPowerOptions for the list of
GDALGridCreate() parameters and invdist for the list
of gdal_grid options.
Moving Average
The Moving Average is a simple data averaging algorithm. It uses a moving window of elliptic form to search values and averages all data points within the window. Search Ellipse can be rotated by specified angle, the center of ellipse located at the grid node. Also the minimum number of data points to average can be set. If there are not enough points in window, the grid node is considered empty and will be filled with specified NODATA value.
Mathematically it can be expressed with the formula:
where:
\(Z\) is a resulting value at the grid node,
\(Z_i\) is a known value at point \(i\),
\(n\) is a number of points in search Search Ellipse.
See GDALGridMovingAverageOptions for the list of GDALGridCreate()
parameters and average for the list of gdal_grid options.
Nearest Neighbor
The Nearest Neighbor method doesn't perform any interpolation or smoothing, it just takes the value of nearest point found in the grid node search ellipse and returns it as a result. If there are no points found, the specified NODATA value will be returned.
See GDALGridNearestNeighborOptions for the list of GDALGridCreate()
parameters and nearest for the list of gdal_grid options.
Data Metrics Computation
All the metrics have the same set controlling options. See the
GDALGridDataMetricsOptions.
Minimum Data Value
Minimum value found in grid node Search Ellipse. If there are no points found, the specified NODATA value will be returned.
where:
\(Z\) is a resulting value at the grid node,
\(Z_i\) is a known value at point \(i\),
\(n\) is a number of points in Search Ellipse.
Maximum Data Value
Maximum value found in grid node Search Ellipse. If there are no points found, the specified NODATA value will be returned.
where:
\(Z\) is a resulting value at the grid node,
\(Z_i\) is a known value at point \(i\),
\(n\) is a number of points in Search Ellipse.
Data Range
A difference between the minimum and maximum values found in grid Search Ellipse. If there are no points found, the specified NODATA value will be returned.
where:
\(Z\) is a resulting value at the grid node,
\(Z_i\) is a known value at point \(i\),
\(n\) is a number of points in Search Ellipse.
Search Ellipse
Search window in gridding algorithms specified in the form of rotated ellipse. It is described by the three parameters:
\(radius_1\) is the first radius (\(x\) axis if rotation angle is 0),
\(radius_2\) is the second radius (\(y\) axis if rotation angle is 0),
\(angle\) is a search ellipse rotation angle (rotated counter clockwise).
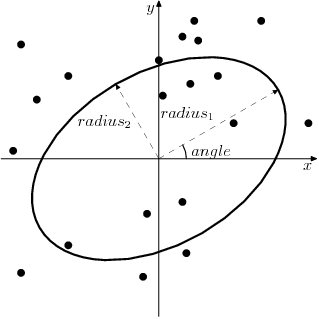
Only points located inside the search ellipse (including its border line) will be used for computation.